3. レポートc(深層学習Day1、Day2)
【深層学習Day1】
Section1:入力層~中間層
- 要点のまとめ
ニューラルネットワークは、入力層、中間層、出力層で構成される。ここでは、入力層から中間層への結合部分を扱う。
入力xiに対して、それぞれ重みwiが与えられる、これにバイアスb を加えたものが中間層に対する入力uとなり、中間層では、シグモイド関数などの活性化関数f(u)により、0~1の間の出力値zに変換される。 式で表すと、u=Wx+b, z=f(u)となる。
- 実装演習結果キャプチャー又はサマリーと考察
1_1_forward_propagation.ipynbを実行。
<2値分類 2-3-1ネットワークを5-10-1に変更>

- 「確認テスト」など自分の考察結果
確認テスト1:入力層x1~x4が動物を表す特徴量となる。
確認テスト2:u1=np.dot(x,W1)+b1
確認テスト3:中間層を表すプログラムを抜粋すると次の箇所である。
# 隠れ層の総出力
z1 = functions.relu(u1)
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
パーセプトロンの実装からスタートしてN.N.の実装を行うので、大変分かりやすかった。
Section2:活性化関数
- 要点のまとめ
N.N.において、次の層への出力を決める非線形の関数で、シグモイド関数やReLU関数が用いられる。シグモイド関数は、微分が元の関数の変形となるため取り扱いが容易である反面、勾配消失問題を引き起こす。その対策としてReLU関数が用いられる。
- 実装演習結果キャプチャー又はサマリーと考察
1_1_forward_propagation.ipynbを実行。
順伝搬(単層・複数ユニット)のプログラム実行結果を表示する。

33行目が中間層出力となるシグモイド関数の出力結果である。
結果出力の中間層出力部を見ると、0~1の間の数値を取っていることが分かる。
- 「確認テスト」など自分の考察結果
確認テスト1:中間層出力の該当箇所は、②で示した通り、
z1=functions.sigmoid(u)となる。
尚、functionsは、配布されたプログラム functions.pyをインポートしたものであるが、そのプログラムの中に、次の通り定義されている。
# 中間層の活性化関数
# シグモイド関数(ロジスティック関数)
def sigmoid(x):
return 1/(1 + np.exp(-x))
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
3.2項活性化関数の中の説明が役に立った。
Section3:出力層
- 要点のまとめ
出力層からは、人間が欲しい形のデータで出力を行う。分類の場合には、正解ラベルによって定義される各クラスの確率を出力させる。誤差関数は、実際にニューラルネットワークを学習させる部分で、はじめは、入力データに対し、出力は訓練データとの誤差が大きな状態であるが、誤差関数が小さくなるように学習をさせる。誤差関数は、二乗誤差などで定義される。尚、ニューラルネットワークの用途別に出力層における、活性化関数と誤差関数の組み合わせは次の通りである。
回帰:恒等写像、二乗誤差
二値分類:シグモイド関数、交差エントロピー
多クラス分類:ソフトマックス関数、交差エントロピー
- 実装演習結果キャプチャー又はサマリーと考察
1_1_forward_propagation.ipynbの他クラス分類(2-3-4ネットワーク)の出力結果及び、出力層の活性化関数と誤差関数の部分のプログラムを抜粋する。
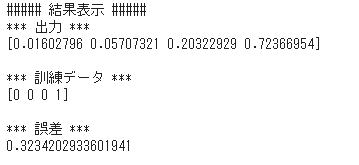
図:出力結果
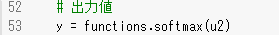
図:活性化関数
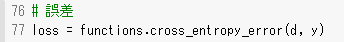
図:誤差関数
- 「確認テスト」など自分の考察結果
確認テスト1
誤差を引き算で定義する場合には、プラスとマイナスの値を取り、合計値が小さくなる場合がある。すなわち差が小さいと判断される。差の二乗を取ると、プラスであろうがマイナスであろうが、差があれば誤差が大きいと判断することができる。頭に1/2をするのは、誤差逆伝搬の計算時で微分を行った時に1となるようにするためである。
確認テスト2
soft max関数のプログラムをfunction.pyにて確認、関数を便利に使うため、ミニバッチ対応及び、オーバフロー対策を付加したコードが書かれてあった。
確認テスト3
交差エントロピーの処理について、function.pyにて確認。x=0で対数関数が-無限大で発散しないように、微小な数値(1-e7)を加える工夫があった。
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
3.2項活性化関数の中の説明が役に立った。
Section4:勾配降下法
- 要点のまとめ
ニューラルネットワークを学習させる手法である。学習とは誤差関数を最小化するようパラメータ(重み、バイアス)を最適化することである。ここで学ぶのは次の3種類である。
・勾配降下法:全データを用いて一気に学習させる。(バッチ学習)
・確率的勾配降下法(SGD):徐々に集まってくるデータにより順次学習させられる(オンライン学習)
・ミニバッチ勾配降下法:オンライン学習の派生版、ランダムに分割したデータ集合(ミニバッチ)により学習を行う。
- 実装演習結果キャプチャー又はサマリーと考察
1_3_stochastic_gradient_descent.ipynbの実行結果。
<確率的勾配降下法>
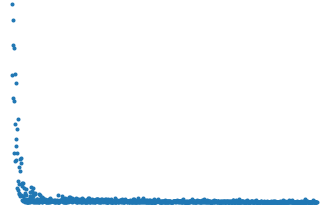
図:結果表示
誤差関数の値が収束していく様子が観測された。
- 「確認テスト」など自分の考察結果
確認テスト1
勾配降下法の該当コード

116、117行目にて、勾配の更新を行っている。
確認テスト2
オンライン学習とは、一度に全てのデータを使って行うバッチ学習と異なり、学習データが得られるたびに、パラメータ更新を行う方法である。
確認テスト3
重みの更新ステップについて、誤差関数の出力結果が重み更新に使用され、次の出力結果を計算、再び、誤差関数の出力結果に基づき、重み更新を行うという流れを理解した。
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
4章、5章にニューラルネットワークの構築から学習について、手順を追って解説されており参考になった。(Section4、5共通)
Section5:誤差逆伝搬法
- 要点のまとめ
誤差逆伝搬法は、パラメータ(重み、バイアス)の更新量を算出するため、誤差を算出し、出力層側から順に微分して、前の層前の層へと伝搬。各パラメータの微分値を解析的に計算する手法である。不要な再帰的計算を避けて微分を算出する。
- 実装演習結果キャプチャー又はサマリーと考察
1_3_stochastic_gradient_descent.ipynbの実行結果
<確率的勾配降下法>
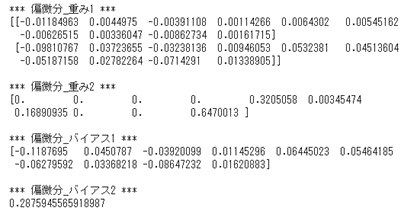
図:学習後の偏微分値
- 「確認テスト」など自分の考察結果
確認テスト
計算結果を保持しているソースコードを添付する。

58行目と66行目にて保持を行っている。
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
4章、5章にニューラルネットワークの構築から学習について、手順を追って解説されており参考になった。(Section4、5共通)
【深層学習Day2】
Section1:勾配消失問題
- 要点のまとめ
誤差逆伝搬法が出力層側から中間層、入力層に遡るにつれて、勾配が緩やかとなり、パラメータがほとんど更新されず、訓練が最適値に収束しなくなる。これは、活性化関数としてシグモイド関数を用いた場合、関数出力が0~1であるのに対し、その微分値の最大値が0.25となることに起因する。解決策としては、活性化関数の選択、重みの初期設定、バッチ正規化が上げられる。
- 実装演習結果キャプチャー又はサマリーと考察
2_2_1_vanishing_gradient.ipynbの実行結果を表示する。
<sigmoid-gauss>
入力層:784、中間層1:40、中間層2:20、出力層10
繰り返し数:2000、ミニバッチ:100、学習率0.1
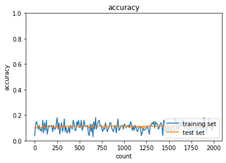
図:学習結果1
勾配消失により精度が上がっていない結果である。
<sigmoid-Xavier(Xavier初期化により勾配消失への対策実施)>
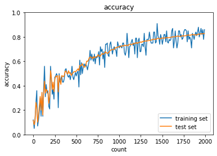
図:学習結果2
Xavier初期化により、学習回数の増加に対し、精度が向上している。
- 「確認テスト」など自分の考察結果
連鎖律の原理を使い、出力側の差分から、上の層に遡って、偏微分値の計算が可能なことを確認した。入力層の偏微分表記が複雑に見えるが、テキストのネットワーク図の出力側から順を追って見ていくと理解は難しくない。
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
勾配消失問題への対応方法として、重みの初期設定が有効であり、現状のベストプラクティスとしては、活性化関数にReLUを使う場合には、「Heの初期値」、sigmoidやtanhなどのS字カーブの場合には、「Xavierの初期値」を使うというところが、特に参考となった。
Section2:学習率最適化手法
- 要点のまとめ
勾配降下法の学習率決定、収束性向上のため以下のようなアルゴリズムが利用されている。通常の勾配降下法が、誤差をパラメータで微分したものと学習率の積を減算するのに対し以下の特徴を持つ。
・Momentum
誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と完成の積を加算する。
・AdaGrad
誤差をパラメータで微分したものと再定義した学習率の積を減算する。
・RMSProp
誤差をパラメータで微分したものと、再定義した学習率の積を減算する。
・Adam
Momentumの過去の勾配の指数関数的減衰平均とRMSPropの過去の勾配の2乗の指数関数的減衰平均の両方を取り扱うものである。
現在は、Adamが使われることが多いとの解説であった。
- 実装演習結果キャプチャー又はサマリーと考察
2_4_optimizer.ipynbの実行結果を表示する
学習率を0.01から0.02に変更、重みの初期化方法を‘Xavier’、バッチ正規化をON
<SDG>
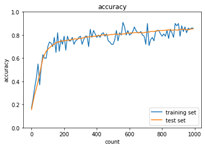
<Momentum>
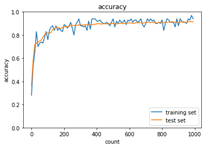
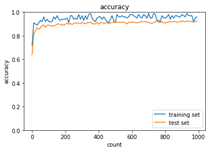
<AdaGrad>
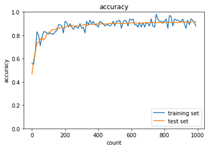
<RSMprop>
<Adam>
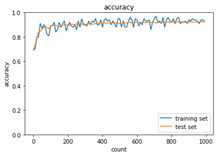
※重みの初期化方法を‘Xavier’を選択した結果、各アルゴリズムで収束するようになった。
- 「確認テスト」など自分の考察結果
確認テスト:モメンタム・Adagrad・RMSPropの簡単な特徴をまとめる
モメンタムは慣性項の追加により、局所的最適解にはならず、大域的最適解となる。谷間についてから、最も低い位置(最適値)に行くまでの時間が早い。AdaGradは勾配の緩やかな斜面に対して、最適値に近づける。ただし、鞍点問題を引き起こすことがある。RMSPropについても、局所的最適解にはならず、大域的最適解となる。ハイパーパラメータの調整が必要な場合が少ない。
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
第6章の「学習に関するテクニック」のところを参考とした。
Section3:過学習
- 要点のまとめ
過学習とは、特定のサンプルに対して、特化して学習した結果、テスト誤差と訓練誤差とで学習曲線が乖離することである。(特定のサンプルでは精度が高いが、他のデータでは精度が落ちる)正則化手法(L1正則化、L2正則化)やドロップアウトと呼ばれる手法を使うことで過学習を防止する。
- 実装演習結果キャプチャー又はサマリーと考察
2_5_overfiting.ipynbの実行結果を表示する。
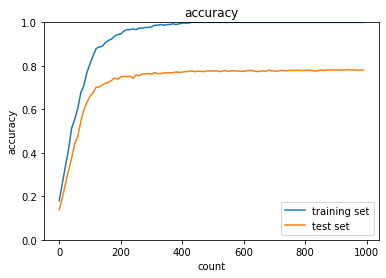
トレーニングセットの精度は高いが、過学習により、テストセットの精度は上がっていない。
- 「確認テスト」など自分の考察結果
線形モデルの正則化手法であるリッジ回帰(L2正則化)の特徴の一つとしては、正則化係数を十分に大きくすると、いくつかの回帰係数は0に近づくが、完全に0とはならない。
尚、ラッソ回帰(L1正則化)においては、正則化係数を十分に大きくすると、いくつかの回帰係数は完全に0となる。
また、L2ノルムは、wの二乗和の平方根、L1ノルムはwの絶対値の和であるため、正則化を表す誤差関数の等高線と制約条件を表すグラフにおいて、L2ノルムでは制約領域が円形、L1ノルムの場合は、ひし形であらわされる。
- 演習問題や参考図書、終了課題など関連記事レポート
リッジ回帰とラッソ回帰のグラフについては、とても難解で分かりにくかったが、次のサイトを参考にイメージとして覚えることとした。本件について、中身を完全に理解して、第3者に分かりやすく説明できるようになることは、今後の課題である。
URL https://qiita.com/MA-fn/items/851f9fc50bda034cd5c6
Section4:畳み込みニューラルネットワークの概念
- 要点のまとめ
畳み込みニューラルネットワークは略してCNNと表記されるが、汎用性が高く、画像認識や音声認識などいたるところで使われている。
- 実装演習結果キャプチャー又はサマリーと考察
2_6_simple_convolution_network_after.ipynbの実行結果を表示する。
<im2colの処理>

フィルタサイズ:3x3、ストライド:1での畳み込み演算結果。
3×3のフィルタで切り出されたデータを一行ずつの行列としてcolに格納。
図:2枚の入力画像のデータに対する処理結果
<CNNの学習結果>
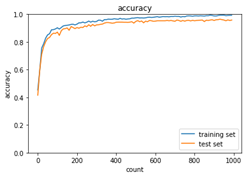
図:学習結果
- 「確認テスト」など自分の考察結果
<Simple convolution network classのプログラム>
class SimpleConvNetの中のレイヤーの構成を表す箇所を抜粋する。

プログラムのプーリング部分を抜粋する。

本プログラムでは、Maxプーリングを適用。
<確認テスト(畳み込み後の画像サイズの計算例)>
サイズ5×5の入力画像を、サイズ3x3のフィルタで畳み込んだ時の出力画像サイズを求める。ストライド2、パディング1とする。
次の公式に当てはめる。 (5+2×1-3)÷2+1=3 答え 3×3
{(画像の高さ+2×パディング高―フィルタ高さ)÷ストライド}+1
- 演習問題や参考図書、終了課題など関連記事レポート
ニューラルネットワークの実装については、次の図書を参考にした。
斎藤康毅:「ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装」、第12版、オライリージャパン(2018)
第7章の「畳み込みニューラルネットワーク」のところを参考とした。
Section5:最新のCNN
- 要点のまとめ
最新のCNNの例として2012年のカナダのトロント大学のSuperVisionチームによるAlexNetが紹介されていた。AlexNetは2012年のILSVRC(ImageNet Large Scale Visual Recognition Challenge)でこれまでの認識率を大きくしのぐ成績で一位となり、画像認識におけるディープラーニングの火付け役となった。224x224の画像を5層の畳み込み層と3層の全結合層から構成される。
- 実装演習結果キャプチャー又はサマリーと考察
CNNのサンプルプログラムとして、2_8_deep_convolution_net.ipynbの実行結果を表示する。(Google Colaboratoryでの実行時間:1時間4分52秒)

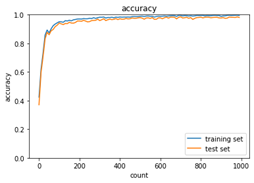
図:学習回数と精度
- 「確認テスト」など自分の考察結果
最終試験等においては、GoogleLeNetの問題がいくつか出された。
Google Netは2014年のILSVRCで一位となった。
AlexNetと比較して、層の数が5層から21層に増えている。Inception moduleやGlobal Average Poolingという手法が適用されている。
Inceptionモジュールの実装により、1×1畳み込みという畳み込みの計算を利用することで、計算効率を上昇させることができる。例えば、2×2、3チャンネルの入力データを1×1畳み込みを行うことで、2x2、1チャンネルのデータに変換する。
Global Average Poolingにより、各チャンネルの画素平均値を求め、各チャンネルの平均値を要素とするベクトルに変換する。
- 演習問題や参考図書、終了課題など関連記事レポート
GoogleNetの原論文
「Going deeper with convolutions」, https://arxiv.org/pdf/1409.4842.pdf
Figure2のInception moduleの模式図、Figure3のGoogLeNetの全体構成などが参考となった。Table2に他のモデルとの認識率の差が記載されているが、、AlexNetの認識率が16.4%であったのに対し、2014年のGoogLeNetでは6.67%に改善されている。
