2. レポートb(機械学習)
(1)線形回帰モデル
①要点のまとめ
1)学習種類:教師あり学習
2)タスク:予測
3)パラメータ推定:最小二乗法・尤度最大化
4)モデル選択・評価:ホールドアウト法、交差検証法
5)概要
説明変数に対して、目的変数が線形であらわされる。線形回帰の応用としては、マーケティング分野における、宣伝費と来店者数の関係の定量評価などで使われる。
②実装演習結果キャプチャー又はサマリーと考察
プログラム名:skl_regression.ipynbをJupiter notebookで実行した結果のキャプチャー
を表示する。
<Boston housing Dataを用いた重回帰分析結果(2変数(犯罪率と部屋の数))>
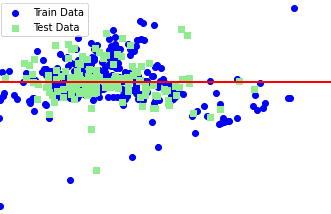
図:学習用と検証用それぞれの残差
④演習問題や参考図書、終了課題など関連記事レポート
動画講義と配布テキストに加え、配布プログラムの実行で内容を十分理解した。
参考図書としては、次を利用した。
加藤公一:「機械学習のエッセンス」、第五刷、pp281-293, SB Creative(2020)
(2)非線形回帰モデル
①要点のまとめ (下記、1)、2)、3)、4)は線形回帰モデルと同じ)
1)学習種類:教師あり学習
2)タスク:予測
3)パラメータ推定:最小二乗法・尤度最大化
4)モデル選択・評価:ホールドアウト法、交差検証法
5)概要
目的変数に対して、目的変数が非線形となる。実装のコーディングでは、モデルの関数の形式を線形で定義するか、非線形で定義するかの差で同じような取り扱いとなる。
非線形関数の場合、関数の次元を上げるなど、表現力を高めて、学習データの残差を小さくすることもできてしまうが、検証用データでは精度が落ちる過学習の問題や、学習データに対して、十分な誤差の得られない未学習の問題に対処する必要がある。
②実装演習結果キャプチャー又はサマリーと考察
プログラム名:skl_nonlinear regression.ipynbをGoogle Colaboratoryで実行した結果のキャプチャーを表示する。
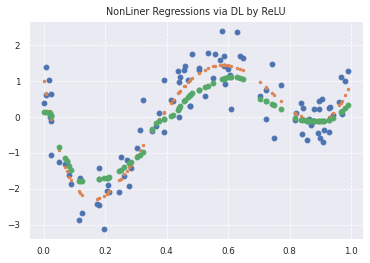
Case 1: Epoch100
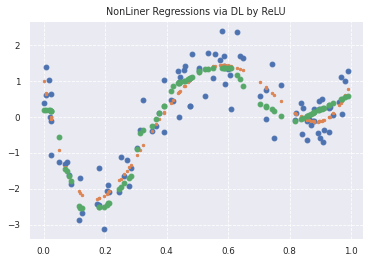
Case2:Epoch200
図:4次の多項式による非線形回帰
青が学習データ(実関数データにノイズを付加して作成)、オレンジが実関数データ、緑が予測値。Epoch数を100から200に上げた結果、x軸の0.0から0.6の区間で予測値が実関数に近づいているように見える。
④演習問題や参考図書、終了課題など関連記事レポート
参考図書としては、次を利用した。
幸谷智紀:「Python数値計算プログラミング」、p181,講談社(2021)
最小二乗法によるフィッテイングのサンプルプログラムを参考に、非線形関数のフィッテイングを試してみた。
(3)ロジスティック回帰モデル
①要点のまとめ
1)学習種類:教師あり学習
2)タスク:分類
3)パラメータ推定:マージン最大化
4)モデル選択・評価:ホールドアウト法、交差検証法
5)概要
ロジスティック回帰は、主に二値分類に使われるアルゴリズムで線形関数の出力をSigmoid関数に入力することで0~1の確率に変換することを特徴とする。重回帰分析では、説明変数に対する目的変数を予測するのに対し、ロジスティック回帰では、事象が起こるか否かの結果を予測するものである。
②実装演習結果キャプチャー又はサマリーと考察
プログラム名:skl_logistic_regression.ipynbをGoogle Colaboratoryで実行した結果のキャプチャーを表示する。
<タイタニック号の乗客データを用いたロジスティック回帰分析結果>
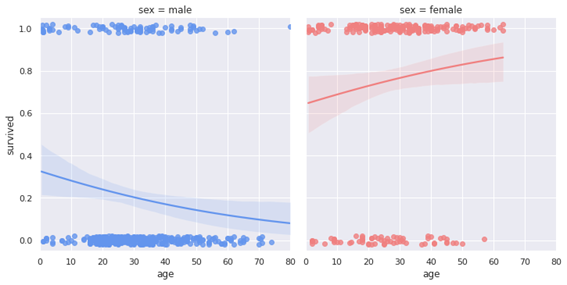
図:性別毎の年齢別生存可能性
男性より女性の方が生存確率は高い。男性は年齢が上がるにつれて生存確率が上がる傾向にあるが、女性の場合は、年齢が上がるほど生存確率が高かったことが図より読み取れる。
④演習問題や参考図書、終了課題など関連記事レポート
参考図書としては、次を利用した。
加藤公一:「機械学習のエッセンス」、第五刷、pp319-325, SB Creative(2020)
(4)主成分分析
①要点のまとめ
1)学習種類:教師なし学習
2)タスク:次元削減
3)パラメータ推定:分散最大化
4)モデル選択・評価:なし
5)概要
主成分分析は多量の成分のデータがあるときに、相関のあるデータの重なりを考慮して、より少ない変数に置き換えることで次元削減を行うものである。
②実装演習結果キャプチャー又はサマリーと考察
プログラム名:skl_pca.ipynbをGoogle Colaboratoryで実行した結果のキャプチャーを表示する。
<scikit-learnによる乳がんデータセットの主成分分析>
オリジナルのホームページ:https://ohke.hateblo.jp/entry/2017/08/11/230000
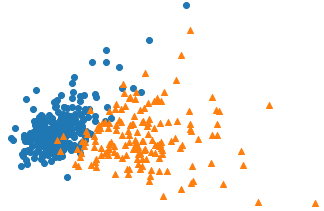
図:次元数を2まで圧縮した散布図(良性を青〇、悪性をオレンジ△)
④演習問題や参考図書、終了課題など関連記事レポート
動画講義と配布テキストに加え、配布プログラムの実行で内容を十分理解した。
参考図書としては、次を利用した。
加藤公一:「機械学習のエッセンス」、第五刷、pp353-359, SB Creative(2020)
(5)アルゴリズム
①要点のまとめ
<アルゴリズム1:k近傍法>
1)学習種類:教師あり学習
2)タスク:分類
3)パラメータ推定:最近傍・K-近傍アルゴリズム
4)モデル選択・評価:なし
5)概要
分類問題のための機械学習手法、最近傍のデータをk個取ってきて、それらがもっとも多く所属するクラスに識別。迷惑メールの分類などに用いられる。
<アルゴリズム2:k-means>
1)学習種類:教師なし学習
2)タスク:クラスタリング
3)パラメータ推定:K-meansアルゴリズム
4)モデル選択・評価:なし
5)概要
与えられたデータをk個のクラスタに分類する。各クラスのクラスタ中心の初期値をk個ランダムにセットした後に、各データ点に対して、各クラスタ中心との距離を計算し、最も距離の近いクラスタを割り当てた後に、各クラスタの中心を新たな中心として、クラスタの再割り当てと、中心の更新を繰り返していく。顧客セグメント分類などに用いられる。
②実装演習結果キャプチャー又はサマリーと考察
プログラム名:①np_knn.ipynb, ②np_kmeans.ipynb, ③skl_kmeans.ipynbをGoogle Colaboratoryで実行。②のキャプチャーを表示する。
<乱数で生成した3グループの分類結果(numpy実装)>
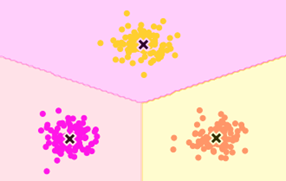
図:クラスタリング結果
④演習問題や参考図書、終了課題など関連記事レポート
k近傍法、k-means法ともに、アルゴリズムは複雑でないので、動画講義と配布テキストに加え、配布プログラムの実行で内容を十分理解した。
参考図書としては、次を利用した。(k-means法)
加藤公一:「機械学習のエッセンス」、第五刷、pp353-359, SB Creative(2020)
(6)サポートベクターマシーン
①要点のまとめ
1)学習種類:教師あり学習
2)タスク:分類
3)パラメータ推定:マージン最大化
4)モデル選択・評価:ホールドアウト検証法、交差検証法
5)概要
2種類のラベルの点のグループをラベルに応じて超平面で分割することで分類する。2次元の場合には直線で分割することとなる。線形分離できない場合でも、特徴空間へ非線形写像を行い線形分離可能とする方法もあり、カーネルトリックと呼ばれる。
②実装演習結果キャプチャー又はサマリーと考察
プログラム名:np_svm.ipynbをGoogle Colaboratoryで実行。キャプチャーを表示する。
<二つのグループを乱数で生成し、ソフトマージンSVMで分類した結果(重なりあり)>
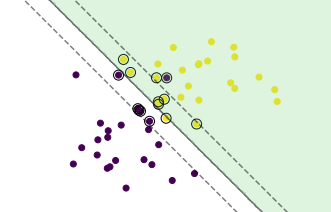
図:ソフトマージンSVM分類結果
④演習問題や参考図書、終了課題など関連記事レポート
動画講義と配布テキストには含まれなかったが、配布プログラムの実行と参考図書により、内容を十分理解した。線形分離の範囲はそれほど難しいものではない。カーネルトリックのサンプルプログラム(ガウシアンカーネル)もやりたいことが理解できていれば、プログラム自体は読めば理解できた。
参考図書としては、次を利用した。
加藤公一:「機械学習のエッセンス」、第五刷、pp325-353, SB Creative(2020)
